Introduction à la transformée de Fourier
Dans beaucoup d'applications, le premier intérêt d'analyser une image n'est pas de retrouver les objets qui la composent (domaine de la reconnaissance de formes), mais plutôt de dégager des degrés de régularité ou de motifs répétés dans cette image. Ces propriétés sont plus facilement analysables dans le domaine des fréquences que dans le domaine spatial. Nous présentons la transfomée de Fourier, introduite en 1822 par Joseph Fourier.
Joseph Fourier
Joseph Fourier est né en 1768 à Auxerre. A l'origine, son étude la plus célèbre concerne la Théorie Analitique de la Chaleur (1822). Le principe est que chaque fonction périodique peut être exprimée comme une somme de sinus et cosinus de fréquences différentes, chacune avec un coefficient. Ce sont les séries de Fourier. Peut importe la complexité de la fonction, tant qu'elle est périodique, elle peut être représentée par une somme.
Cette découverte était révolutionnaire à l'époque. Les fonctions non périodiques peuvent également être exprimées sous la forme d'une intégrale de sinus et/ou cosinus pondérée par une fonction. C'est la transformée de Fourier.
L'une des caractéristiques principales est qu'il est possible, lorsqu'on est dans le domaine des fréquences, de repasser dans le domaine temporel par la transformée de Fourier inverse sans aucune perte d'informations. Certains problèmes sont plus facilement solvables dans le domaine fréquentiel !
Ilustration
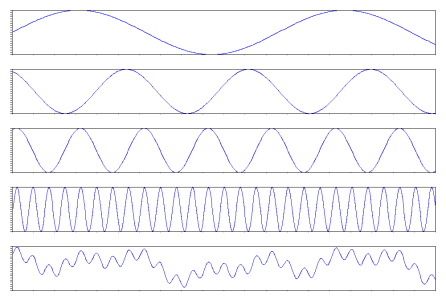
On illustre ci-dessous la somme de 4 sinusoïdes composant la 5ème.
