Introduction à la synthèse d'un océan
Réaliser la simulation de fluides à grande échelle est un challenge qui a suscité de nombreuses études. Pour avoir un résultat réaliste, des procédés complexes ont été mis en oeuvre, chacun exploitant des théories relativement différentes. Nous allons nous pencher sur l'utilisation de la Transformée de Fourier pour synthétiser la surface d'un océan.
Présentation
On connaît plusieurs méthodes pour la simulation de fluides :
- Domaine spatial
- Approche physique : méthode numérique qui se base sur les équations de Navier-Stokes [CFD (Computation Fluid Dynamics)]. La méthode est appliquée sur une grille eulérienne 2D ou 3D mais reste limitée à des zones de taille réduite car elle impose un grand nombre de calculs. L’usage des logiciels CFD actuels s’avère gourmand en temps et nécessite une attention particulière (concernant les géométries correctes et les conditions aux limites).
- Approche des particules hydrodynamiques : [ SPH (Smoothed Particle Hydrodynamics)]
Approche CFDApproche SPH - Domaine fréquentiel
- Approche réduite/ Approche spectrale : celle que nous présentons ici pour ne modéliser que la surface de la mer.
En choisissant de ne modéliser que la surface de la mer, on s'affranchit de nombreux calculs et on gagne un temps précieux (utile pour des applications en temps réel).
La surface de la mer
La surface de la mer est constituée de vagues produites par le vent. On définit la longueur d'onde comme la distance entre deux crêtes de vagues. La hauteur des vagues est aléatoire. On définit aussi la notion de champ :
Un champ contient une somme d'octaves (fréquences harmoniques) de "vagues" sinusoïdales. Plus on ajoute de sinusoïdes au modèle, plus la surface paraîtra réaliste. Ainsi, on a déjà l'intuition que la formule de la transformée de Fourier (TF) qui contient une somme de sinusoïdes peut nous aider.
Grâce à la transformée de Fourier et notamment sa propriété de périodicité, nous allons voir comment animer un champ 2D
- raccordable dans l'espace et le temps (on peut créer puis dupliquer un seul champ de manière continue)
- facilement contrôlable (taille, résolution)
On utilisera plus précisément la transformée de Fourier inverse qui, à partir d'un champ de fréquences, permet de retrouver le champ spatio-temporel. Rappelons que nous travaillons dans le cas discret.
Définition de la transformée de Fourier 2D dans notre étude
Pour une modélisation d'une mer, on va considérer une grille 3D pour laquelle la hauteur au point 
est une valeur 
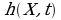au temps t et dont la définition est :
où :
- est la position d'un point
est un vecteur 2D 
pointant dans la direction de la vague de vitesse 
est le temps
est la hauteur d'une vague à la position X en fonction de t dans le domaine spatial
est la valeur du signal dans le domaine fréquentiel
Le champ 3D est créé à partir d'un champ fréquentiel. Il faut donc créer ce champ (amplitudes et phases).
Note : Cette technique a été utilisée pour la modélisation de la mer dans des films tels que Titanic de James Cameron, ou Waterworld de Kevin Reynolds.
