Propriétés de la transformée de Fourier
Linéarité
Si un signal x(t) est une combinaison linéaire de signaux si(t), le spectre X(f) est une combinaison linéaire des spectres Si(f):
![]()
Séparabilité
Si l’image f(x,y) est spatialement séparable, c’est-à-dire
![]()
alors
![]()
Dans ce cas, la transformée de Fourier de l’image ¡f(x,y) est égale au produit des transformées de Fourier unidimensionnelles des fonctions f1(x) et ¡f2(y)
Translation
Comme quand on travaille à une dimension, une relation simple peut être déduite par déphasage d'une image dans un domaine ou dans l'autre. Sachant que les deux domaines sont considérés périodiques pour les fins de la transformée, le déphasage revient à une rotation autour des limites. Un déplacement/glissement dans un des domaines correspond à un déphasage dans l'autre – si un élément se déplace dans le domaine spatial, dans le domaine fréquentiel le spectre d'amplitude reste inchangée, mais sa phase se décale proportionnellement. Voici les équations décrivant ce phénomène.
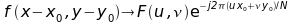 |
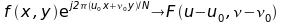 |
Translation spatiale |
Translation fréquentielle |
Échelle
Plus un signal "est large", plus son spectre "est étroit"
Comme c'est le cas à une dimension, le rétrécissement dans un domaine provoque l'expansion dans l'autre. Ceci veut dire que lorsqu'un objet grandit sur une image, les traits correspondants dans le domaine fréquentiel vont rétrécir (proportion inverse). L'équation qui définit ceci:
![]()
Aspect matriciel de la transformation. Rotation
Cette propriété n'a pas d'analogue unidimensionnel. Puisque les équations de la transformée sont séparables, la position du contenu dans le domaine fréquentiel est basée sur la position du contenu dans le domaine spatial. Cela signifie que la rotation dans le domaine spatial engendre une rotation dans le domaine fréquentiel. Les équations suivantes décrivent cette relation:

Relations de parité
Pour finir, il est important de savoir que la transformée de Fourier d'une fonction paire (symétrique pour les temps positifs et négatifs) est purement réelle, alors que celle d'une fonction impaire est purement imaginaire. De même la transformée de Fourier d'une fonction purement réelle sera paire. Ceci nous rappelle que pour obtenir une discrimination du signe des fréquences dans le spectre, il faut avoir une détection complexe.
f(t) |
F(u) |
réelle, paire |
réelle, paire |
réelle, impaire |
imaginaire, impaire |
imaginaire, paire |
imaginaire, paire |
imaginaire, impaire |
réelle, impaire |
complexe, paire |
complexe, paire |
complexe, impaire |
complexe, impaire |
Illustration
Les propriétés de translation, d'échelle et de rotation matricielle sont illustrées dans l'animation ci-dessous :

De gauche à droite: spectre de phase, image d'origine, transformée de Fourier
Symétrie hermitienne
On appelle symétrie hermitienne lorsque la partie réelle est symétrique et que la partie imaginaire est antisymétrique. On montre facilement que si x(t) est réel, sa transformée X(v) possède une symétrie Hermitienne :
![]()
c'est à dire ![]()
