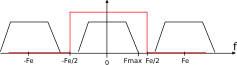
Propriétés : Inversibilité et dérivation
Inversibilité
La transformation est inversible :
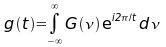
et son inverse est pratiquement identique à la transformation initiale (à un retournement près). C'est à dire que non seulement il est possible, à partir d'une fonction continue, d'obtenir son spectre, mais que d'autre part il est possible de re-synthétiser complètement la fonction initiale à partir de son spectre.
est la fréquence d’échantillonnage.
Dérivation
Si la fonction g(t) est dérivable, alors sa dérivée possède la transformée de Fourier suivante :
Cette relation montre que plus une fonction est "lisse" (dérivées faibles) plus sa transformée décroît rapidement vers zéro à l'infini, et d'autre part, que, plus les valeurs d'une fonction sont concentrées autour de l'origine, plus celles de sa transformée sont, au contraire, étalées.
Egalités de Parseval – Plancherel
La transformation de Fourier transforme le produit de convolution en produit simple et le produit en produit de convolution = une autre formulation de la loi de conservation de l'énergie
