Protocole de création de l'océan
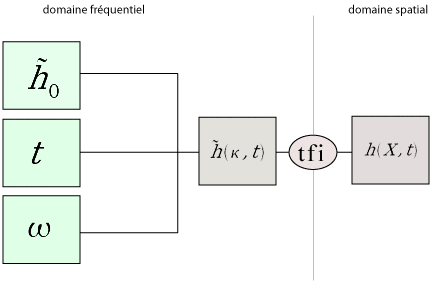
On a vu qu'une carte de hauteur peut être générée pour créer un océan à partir d'une somme de sinusoïdes. On utilise pour cela la transformée de Fourier inverse. Il faut donc lui fournir un champ fréquentiel 
.
Création du champ des fréquences
La génération du champ de fréquence à chaque instant t est définie par :
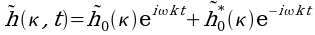
où :
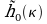est la fréquence initiale (à l'instant t0=0s).-
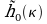est le conjugué de , ce qui signifie que 
.
Cette relation préserve la propriété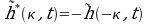
qui nous permet de calculer puis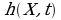 
avec la transformée de Fourier inverse en une seule fois (on ne calcule pas le conjugué, puisqu'on connaît déjà sa valeur...) pour un t donné. 
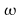est la fréquence angulaire qui détermine la dispersion de la vague. 
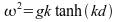où d est la profondeur de la mer, k la vague, et 
la constante de gravitation de Newton (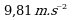
).
Note : Dans la cas de l'océan, on se situe en eau profonde, on peut donc réduite la formule à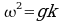 
.
Champ de fréquence initial
Pour partir d'une base (quel champ fréquentiel donné à la transformée de Fourier inverse), on se base sur la définition suivante :
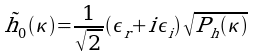
pour le complexe (Re, Im) donné. C'est ici qu'intervient la donnée physiquement intéressante, à la base de laquelle c'est bien une mer qu'on modélise et non un simple bruit aléatoire. Le terme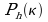 
est basé sur des études théoriques et empiriques océanographiques et définit le bruit initial par le spectre de Phillips. Les coefficients du spectre de Phillips sont deux valeurs aléatoire gaussiennes (de moyenne égale à 0 et d'écart-type égal à 1) indépendantes. Cela permet d'avoir une distribution moyenne des vagues (on peut utiliser une distribution différente, par exemple logarithmique, pour obtenir des vagues soit très hautes ou très basses, mais avec peu d'alternatives au milieu).
Protocole de création
A partir du champ de fréquences initial, de t et de w on détermine la formule du champ de fréquences général. Grâce à la transformée de Fourier inverse, on traduit les données fréquentielles en données spatiales et on obtient une image 2D qu'on utilise comme carte de hauteur pour notre océan.
Présentation des cartes de hauteur
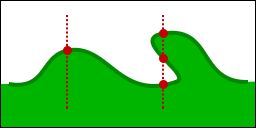
Une carte de hauteur est une image 2D généralement en niveaux de gris, dont la valeur au pixel (i,j) détermine la hauteur d'un plan au point (n,m), où n=k.i et m=l.j.
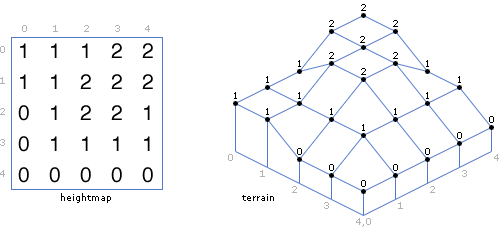
Elles sont particulièrement adaptées aux rendus de terrains, mais ne permettent pas d'attribuer plus d'une hauteur par point de la carte (donc on ne peut pas modéliser les creux de vagues par exemple).
