Spectre de Phillips
Une carte de hauteurs peut être générée pour créer un océan à partir d'une somme de sinusoïdes. On utilise pour cela la transformée de Fourier inverse à qui on fournit un champ fréquentiel. Nous basons notre cas sur des études théoriques et empiriques océanographiques pour introduire le spectre de Phillips.
Présentation du spectre de Phillips
Si on regarde bien la surface de la mer, elle semble composée de vagues "aléatoires" de longueur d'onde et de période différentes. Pour représenter cette surface, on peut utiliser un spectre de vagues qui donne la distribution de l'énergie des vagues selon différentes fréquences ou longueurs d'ondes de la surface. On retrouve le concept de spectre de la théorie de Fourier (1768-1830) qui montre que chaque signal peut-être assimilé à une somme (infinie) de fonctions sinusoïdales entre un certain intervalle.
L'analyse photographique et les mesures radar de la surface des océans ont montré que l'amplitude des vagues est statistiquement stationnaire selon un spectre. Plusieurs modèles analytiques et semi-empiriques existent pour le représenter. Dans le cas de la mer, il faut prendre en compte plusieurs paramètres (notamment le vent, la longueur d'onde de chaque vague [qui est en soi, une onde !]).
Définition
On utilise un modèle prouvé, le spectre de Phillips défini par :
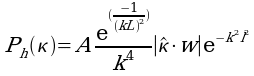
où :
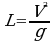 est la longueur d'onde maximum pour un temps continu à la vitesse V du vent.
est la longueur d'onde maximum pour un temps continu à la vitesse V du vent.- A est une constante numérique affectant l'ensemble des hauteurs.
- l'exposant au dénominateur
 permet par exemple de changer la physionomie parallèle de la mer.
permet par exemple de changer la physionomie parallèle de la mer. - le terme
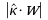 permet d'éliminer les mouvements perpendiculaires à la direction du vent w, k étant la direction de la vague.
permet d'éliminer les mouvements perpendiculaires à la direction du vent w, k étant la direction de la vague. - le terme
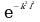 permet enfin d'éliminer les longueurs d'ondes inférieures à l (
permet enfin d'éliminer les longueurs d'ondes inférieures à l (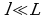 ) : on améliore la convergence du spectre.
) : on améliore la convergence du spectre.
Une fois toutes ces données déterminées on peut réaliser la transformée de Fourier inverse et ainsi générer le champ de hauteurs.
Discussion autour du spectre de la mer
Les études réalisées montrent que sur un temps long et une surface large, les vagues de la mer sont relativement redondantes et rendent notre modèle correct.
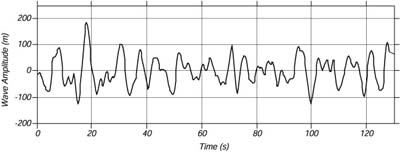
Enregistrement de l'amplitude d'une vague - Atlantique Nord
Comment se créent les vagues ?
Les vagues sont liées au vent. On dénombre trois processus physiques qui se mettent en route lorsque le vent se met à souffler :
- Pressions alétoires à la surface de l'océan, qui produisent des petites vagues aux longueurs d'ondes limitées
- Ensuite, le vent agit sur ces petites vagues, et les rend plus larges. Le souffle du vent sur ces vagues provoque des pressions différentes qui augmentent la taille des vagues de manière exponentielle (processus instable).
- Enfin, les vagues interagissent les unes avec les autres, ce qui permet des transferts d'énergie entre les vagues. Pierson et Moskowitz notent que ce processus peut engendrer que la vitesse des vagues soit plus importante que celle du vent.
Comment déterminer le spectre de la mer ?
Pour déterminer un spectre de la mer, on numérise une suite de données représentant l'amplitude de la mer à coordonnées fixes. On calcule ensuite la transformée de Fourier de la série, puis le périodogramme (à partir de la somme au carré des parties réelles et imaginaires de la transformée de Fourier). On moyenne ainsi plusieurs périodogrammes et on détermine la distribution de l'énergie.
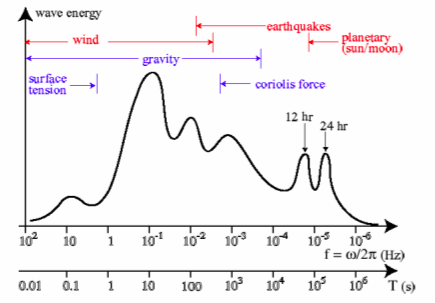
Spectre de mer (en rouge : processus de création, en bleu : forces)
Bien sûr, cette méthode est incomplète pour décrire chaque interaction, mais les résultats sont globalement satisfaisants.
Autres représentations spectrales
Le plus simple ? Pierson et Moskowitz (1964)
Cette méthode se base sur le fait que si le vent souffle de manière constante sur une large surface, alors les vagues et le vent vont être en "équilibre".
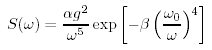
où ω = 2πf est la fréquence de la vague (Hz).
Le spectre JONSWAP (Joint North Sea Wave Project)
Cas plus général que le spectre de Pierson-Moskowitz puisqu'il prend en compte le facteur de réhaussement
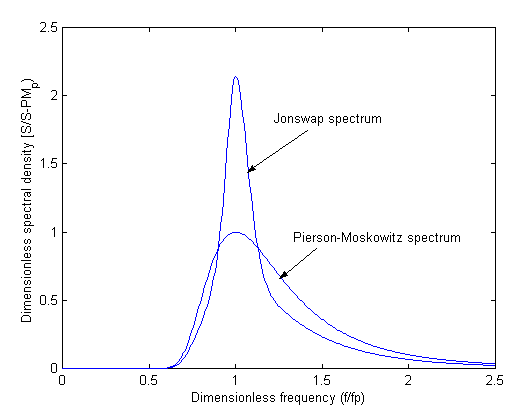
Spectres de Pierson-Moskowitz / JONSWAP .
Spectre JONSWAP sous Matlab
